Capitolo 3 Le librerie VTK
I programmi
sviluppati nell’ambito di questa tesi fanno uso delle librerie VTK, acronimo di
“The Visualization Toolkit”. La scelta
di questo strumento e’ stata determinata dalle sue capacità in termini di
visualizzazione scientifica (già di per sé utili allo svolgimento di questa
tesi), dalla possibilità di estendere e
introdurre nuove funzionalità di base agendo direttamente sul codice sorgente
distribuito nella forma “open source” e di realizzare applicazioni
cross-platform.
Lo scopo di questo capitolo è di dare una panoramica di VTK entrando nei dettagli solo dove ciò è richiesto per la comprensione del codice riportato in appendice, per approfondimenti si rimanda alla documentazione ufficiale [VTK].
La versione di VTK impiegata è la 2.2.
3.1 Introduzione
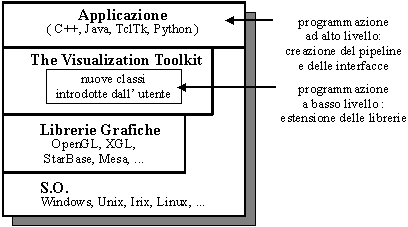
Il VTK comprende un insieme di librerie di classi scritte in C++ e alcuni “wrappers” che ne permettono l’utilizzo anche dai linguaggi Java, TclTk e Python. E’ inoltre possibile esportare le scene prodotte come file in formato VRML.
Il codice delle librerie è portatile, previa ricompilazione queste possono girare sotto Windows e sotto le principali piattaforme Unix-like.
VTK richiede la presenza di una libreria grafica, come OpenGL, XGL, Mesa o StarBase.
Le classi fornite sono più di cinquecento, possiamo vederle organizzate in tre gruppi:
·
Classi
del Visualization Pipeline
Comprendono “Data Objects” e “Process Objects”.
I Data Object incapsulano i dati e definiscono i metodi per accederli, i
Process Object ricevono un Data Object in ingresso e ne producono uno nuovo in
uscita.
Istanziando e collegando opportuni Process Object si costruisce il
visualization pipeline che ha il compito di trasformare i dati in primitive
grafiche. Il Visualization Pipeline è presentato nel paragrafo 2.
·
Classi
del Graphics Pipeline
Comprendono classi che rappresentano le entità’
necessarie alla creazione di una scena tridimensionale quali luci, camera ed
attori.
Mediante il graphic pipeline si trasformano le primitive grafiche in una
rappresentazione della scena che può essere esplorata interattivamente.
Queste classi sono introdotte nel paragrafo 3
·
Classi
dell’ Imaging Pipeline
Sono un sottoinsieme delle classi nel Visualization
Pipeline, con ruoli analoghi ma specializzate per il trattamento delle
immagini, offrono caratteristiche avanzate come il supporto di “streaming”,
“caching”, e “multithreading”. Queste classi sono state usate in minima parte e
non saranno ulteriormente citate.
|
|
L’utilizzo di VTK prevede due diversi livelli di astrazione
·
Programmazione
ad alto livello
In cui si costruiscono l’interfaccia dell’applicazione
e il pipeline. Quest’ultimo viene composto usando le classi del VTK come
blocchi elementari, a questo scopo si può usare un linguaggio interpretato
senza compromettere le prestazioni.
·
Programmazione
basso livello
Per soddisfare particolari esigenze le librerie
possono essere estese inserendo nuove classi. L’ottima documentazione fornita
semplifica molto questo compito.
3.2 Visualization Pipeline
Contrariamente all’uso comune nella programmazione Object Oriented in VTK si è scelto di separare i dati dalle procedure che li elaborano.
I dati sono incapsulati nei Data Objects, le procedure nei Process Objects.
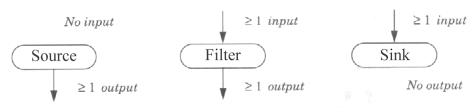
I Process Object si dividono in Source, Filter e Sink a seconda della presenza di uno o più input o output come illustrato nella figura seguente.
|
Figura 1‑2 Tipi di Process Object |
I Source Object sono oggetti che producono un Data Object leggendolo da un File (Reader) oppure costruendolo mediante una procedura (Procedural Source).
I Sink Object esportano Data Object su di un file (Writer) oppure verso il Graphics Pipeline (Mapper).
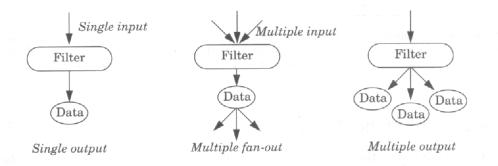
Gli Oggetti di tipo Filter possono avere più input e produrre più output, un singolo output può essere usato come input da più filtri (Multiple fan out).
|
Figura 1‑3 Molteplicità degli ingressi e delle uscite |
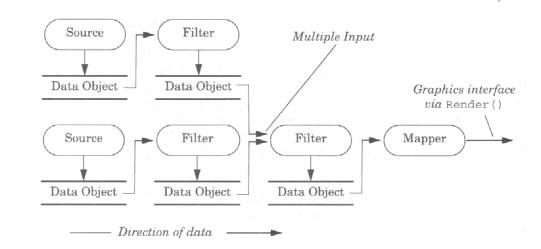
La figura seguente illustra un primo esempio di Pipeline (data flow network), nel seguito per semplicità i Data Object non verranno esplicitamente rappresentati.
|
Figura 1‑4 - esempio di Pipeline |
La connessione tra due Process Object avviene di solito tramite l’istruzione
Filtro2->SetInput( Filtro1->GetOutput());
Per Filtri con più entrate o uscite esistono forme di sintassi analoghe.
Le connessioni sono tipizzate, si possono agganciare solo Process Object che si scambiano un Data Object di tipo compatibile,
Affinché il Pipeline produca il risultato atteso occorre che tutti i Process Object vengano mandati in esecuzione, l’intero processo è chiamato “esecuzione del pipeline”.
Il controllo dell’esecuzione del Pipeline è di tipo “Demand Driven”, tipicamente l’utente chiede l’aggiornamento dello schermo e questo provoca la richiesta dei dati, si assume che in generale i dati non sono pronti e quindi prima di usarli bisogna chiamarne il metodo Update.
Il metodo Update è implementato sia nei Data Object che nei Process Object e realizza un meccanismo di sincronizzazione implicito.
Una volta invocato il metodo Update, la pipeline viene percorsa a ritroso fino ad individuare il primo elemento necessario di (ri)calcolo (in genere un Source Object). Per evitare elaborazioni inutili è previsto che ciascun Process Object vada in esecuzione solo se ci sono state modifiche nei suoi parametri o nei suoi input.
Questo schema di funzionamento supporta senza problemi anche strutture pipeline che contengono dei loop.
3.3 Graphics Pipeline
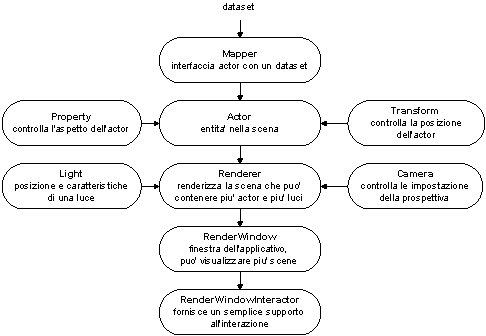
É d’uso comune nella computer grafica descrivere una scena tridimensionale mediante la metafora del set cinematografico, cosi anche in VTK troviamo gli oggetti Actor, Light e Camera. Questi e gli altri oggetti che compongono il graphics pipeline sono illustrati nella figura che segue
|
Figura 1‑5: il Graphics Pipeline |
Gli attori rappresentano le entità’ visibili nella scena e sono biunivocamente associati ai mappers che ne forniscono la rappresentazione grafica.
Un attore rappresenta la propria posizione nello spazio, l’orientamento e la scala mediante un oggetto Transform che incapsula una matrice 4x4, l’aspetto è controllato mediante un oggetto Property che ne stabilisce le caratteristiche di superficie (colore ambiente, diffuso e speculare, trasparenza) e il tipo di rendering (solido, wireframe).
L’oggetto Camera stabilisce in che modo la scena viene proiettata sull’immagine, sono disponibili la proiezione parallela e prospettica, è possibile abilitare la modalità di resa stereo se si dispone delle risorse necessarie.
Gli attori, le luci, e la camera sono poi passati ad un oggetto Renderer che crea l’immagine della scena. L’oggetto RenderWindow rappresenta una finestra dell’applicativo e può essere suddiviso in più quadranti per visualizzare una o più scene. Infine l’oggetto RenderWindowInteractor fornisce un semplice supporto per l’interazione, tramite il mouse è possibile ruotare, traslare e fare uno zoom sia della vista che dei singoli attori.
Citiamo brevemente le classi Actor2D, property2D, mapper2D che rappresentano oggetti bidimensionali utili per inserire etichette o didascalie nella scena, LODActor cambia dinamicamente il tipo di rappresentazione (Solid, WireFrame, BoundBox) in modo da garantire comunque un adeguato feedback durante l’interazione.
Gli oggetti RenderWindow e RenderWindowInteractor permettono di gestire le finestre di visualizzazione e gli eventi ad esse connesse in maniera indipendente dalla piattaforma.
Tipi più specializzati di questi oggetti sono implementati nei vari wrapper di VTK ad esempio RenderWidget è disponibile solo da TCL e consente di inserire una RenderWindow nelle interfacce come se fosse un normale widget.
Il seguente frammento di codice TCL costruisce un esempio di graphics pipeline e mostra i metodi utilizzati per realizzare i collegamenti.
...
VtkMapper
Mapper
Mapper SetInput a_DataSet
vtkActor Actor
Actor SetMapper Mapper
vtkCamera
Camera
vtkLight Light
vtkRenderer Renderer
renderer AddActor Actor
Renderer SetActiveCamera Camera
Renderer AddLight Light
vtkRenderWindow
RenWin
RenWin AddRenderer Renderer
vtkRenderWindowInteractor
IRenWin
IRenWin SetRenderWindow RenWin
...
3.4 Data Objects
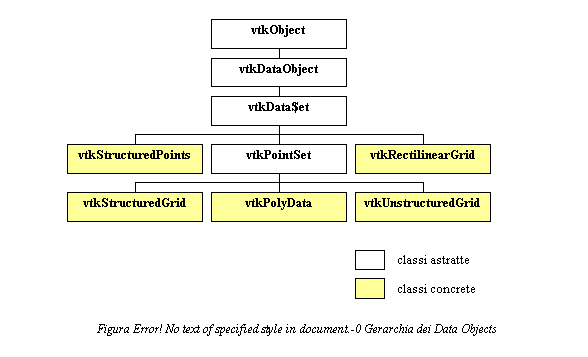
La figura seguente illustra la gerarchia dei Data Objects, gli
oggetti che rappresentano i dati.
Tutte le classi di VTK derivano da vtkObject che fornisce alcune funzionalità di base (supporto al Debugging, al Reference Counting ed altro) , la classe vtkDataObject definisce in che modo sono gestiti e come si possono accedere i Field ( vedere il paragrafo sugli attributi ), proseguendo lungo la gerarchia abbiamo la classe vtkDataSet di cui parleremo nel resto del paragrafo, i tipi concreti di DataSet saranno presentati nel paragrafo 7.
La classe vtkDataSet esprime “il modello astratto” dei dati e provvede una interfaccia uniforme per accederli.
L’intenzione dei progettisti di VTK era di ottenere un modello molto generale, cioè in grado di rappresentare con facilità molte tipologie di dati diverse, per questo motivo nel progetto del modello sono partiti da due semplici osservazioni: “i dati sono discreti” e “i dati tendono ad essere di grandi dimensioni”.
Affinché una certa informazione possa essere rappresentata mediante un calcolatore deve essere portata in forma discreta, il processo di discretizzazione induce nei dati una particolare organizzazione, illustrata nello schema che segue.
|
Topologia proprieta’ delle celle Geometria proprieta’ dei vertici Si partiziona il dominio in celle e si misurano le
grandezze in corrispondenza dei vertici Attributi L’insieme delle misure Struttura Rappresentazione
discreta dell’informazione Discretizzazione o campionamento Informazione Una o piu’ grandezze che variano in un certo dominio |
Questa organizzazione prevede che un DataSet comprenda struttura ed attributi, la struttura a sua volta è espressa in termini di topologia e geometria, per chiarire questi ultimi due termini ne ricordiamo la definizione.
Topologia : L’insieme delle proprietà invarianti
rispetto a certe trasformazioni, nel nostro caso le trasformazioni sono la
traslazione, la rotazione e la scalatura non uniforme.
Geometria : Una
particolare istanza di una topologia.
Esempio: Definire una forma triangolare, e quindi affermare implicitamente che si tratta di una figura piana con tre vertici e tre lati, equivale a specificarne la topologia. Assegnare le coordinate ai vertici equivale a specificarne la geometria.
La struttura del DataSet fornisce supporto a due importanti operazioni:
L’attraversamento ( data traversing )
Una delle funzioni delle celle è quella di
esprimere le relazioni di adiacenza tra i vertici, è così possibile percorrere
la struttura lungo qualsiasi direzione. Sul data traversing si basano molti
algoritmi come ad esempio la verifica di connessione, o la semplificazione
delle superfici (decimazione).
L’interpolazione
L’uso dell’interpolazione permette di ottenere un valore approssimato delle grandezze rappresentate nel DataSet in qualsiasi punto del dominio.
Come sappiamo il valore esatto è noto solo in corrispondenza dei vertici, se interroghiamo il DataSet in corrispondenza di un punto p diverso da un vertice ma interno ad una cella, da questa possiamo risalire ai valori contenuti nei vertici ed interpolarli, l’approssimazione che si commette dipende dalla densità della struttura e dalla velocità di variazione delle grandezze.
Gli attributi sono le misure effettuate, più frequentemente sono associate ai vertici ma questo non è l’unico caso, la misura di una massa potrebbe venire associata alle celle mentre la misura di un flusso sarà probabilmente associata ad una faccia. In certi casi gli attributi possono essere assenti, per esempio se stiamo rappresentando una superficie nello spazio questa sarà tradotta in una “mesh” di poligoni e quindi l’informazione viene catturata nei soli termini di struttura.
Veniamo adesso al secondo punto, dall’osservazione che i dati tendono ad essere di grandi dimensioni nasce l’esigenza di usare rappresentazioni compatte ed efficienti. A questo scopo dove è possibile si usano rappresentazioni della struttura implicite, dove non è possibile si usano organizzazioni basate su array, sono anche supportate funzionalità per il caching e la condivisione dei dati.
Rappresentazione implicita
Se la struttura presenta delle regolarità alcune sue parti possono essere più convenientemente rappresentata in forma implicita.
Per esempio un reticolo a maglie quadre e vertici equidistanziati presenta regolarità sia nella geometria che nella topologia. Per rappresentare la geometria è sufficiente ricordare il numero di vertici lungo ogni direzione, la spaziatura e l’origine del reticolo, mediante semplici formule è possibile passare dalle coordinate di reticolo alle coordinate spaziali dei vertici.
Per rappresentare la topologia possiamo ancora trovare delle formule che legano una particolare cella ai suoi vertici e dal momento che le celle sono tutte uguali le restanti proprietà saranno memorizzate una volta sola.
Organizzazioni basate su array
Alla base di molte delle strutture dati del VTK troviamo la classe vtkDataArray che rappresenta un vettore di celle adiacenti di memoria. Rispetto alle possibili alternative quali l’uso di liste o di array di puntatori a strutture gli array possono essere creati, distrutti e attraversati piu velocemente e richiedono minore spazio di memoria.
Questa scelta penalizza la possibilità di editare o modificare singole parti del DataSet ma nell’ambito della visualizzazione scientifica questa possibilità è considerata di secondaria importanza essendo l’obbiettivo principale quello di esplorare, rappresentare e interpretare informazioni nella loro forma complessiva.
Tra le conseguenze di questa scelta abbiamo che in VTK l’accesso a tutte le entità avviene tramite indici.
Caching
Trovare il giusto compromesso tra l’uso della memoria il tempo richiesto dall’elaborazione costituisce un tema importante nell’ambito della visualizzazione. Nel Visualization Pipeline presentato precedentemente si è supposto che gli output dei vari filtri fossero sempre disponibili, tuttavia conservare tutti i risultati intermedi di una elaborazione può essere troppo costoso in termini di memoria. L’ approccio alternativo è quello di conservare l’output di un Filtro solo per il tempo in cui è necessario al filtro successivo ma questo comporta ulteriori elaborazioni ogni volta che il Pipeline va in esecuzione.
In VTK si può assegnare una delle due strategie a ciascuno dei filtri, quale sia da preferirsi dipende dalla dimensione dei dati e dalla frequenza con cui il ramo del pipeline interessato viene eseguito.
Condivisione
dei dati
Un altro modo per ridurre la richiesta di memoria è quello di permettere la condivisione di strutture usando il reference counting. Ad esempio se un certo filtro altera solo gli attributi il DataSet prodotto in uscita può usare la struttura del DataSet in input. Le funzionalità relative al reference counting sono implementate nella classe vtkReferenceCount da cui discendono molte delle classi di VTK.
Vediamo adesso i principali metodi esposti dalla classe vtkDataSet.
|
Metodi relativi alla Geometria Int GetNumberOfPoints()
Float
*GetPoint(int ) supporto per l’accesso ai vertici float
*GetBounds(),float *GetCenter(),float GetLength() GetLenght restituisce la diagonale del Bounding Box Void
GetPointCells(int ,vtkIdList *) accesso alle celle che usano un certo vertice int FindPoint(…) individua il vertice piu vicino ad una certa posizione |
|
Metodi relativi alla Topologia Int
GetNumberOfCells() VtkCell
*GetCell(int ) supporto per l’accesso alle celle void
GetCellPoints(int ,vtkIdList *) accesso ai vertici usati da una certa cella void GetCellNeighbors(…) accesso alle celle adiacenti int FindCell(…) individua la cella che contiene una certa posizione |
|
Metodi relativi agli Attributi VtkCellData *GetCellData() accesso agli attributi associati ai vertici vtkPointData *GetPointData() accesso agli attributi associati alle celle |
3.5 Tipi di Celle
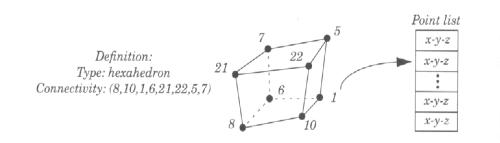
Una cella viene specificata indicandone il tipo ed una lista ordinata di identificatori di vertici detta connectivity list.
|
Figura 1‑6 – esempio di cella |
Dalla specifica del tipo deriva implicitamente
la topologia della cella cioè il numero dei vertici, dei lati e delle facce, le
relazioni di appartenenza e di adiacenza tra queste entità. La connectivity
list invece fornisce la geometria della cella, infatti attraverso gli indici
dei vertici è possibile individuarne le coordinate.
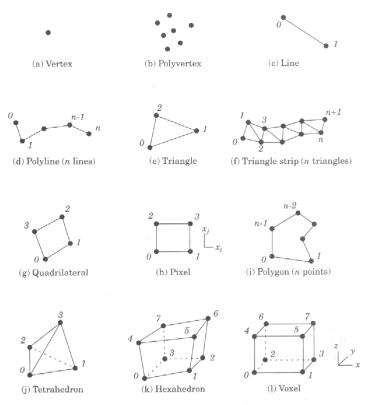
|
Figura 1‑7 tipi di celle supportati da VTK. |
I tipi di celle si dividono in elementari e composte, le celle composte sono costituite aggregando celle elementari e sono d’uso comune nelle librerie OpenGL.
Nella tabella seguente sono riportati i tipi di cella forniti da VTK.
Tabella 1
|
|
Elementari |
Composte |
|
|
Dimensione topologica |
0D |
VtkVertex |
VtkPolyVertex |
|
1D |
VtkLine |
VtkPolyLine |
|
|
2D |
VtkTriangle |
VtkTriangle
Strip |
|
|
3D |
VtkThetrahedron VtkHexahedron VtkVoxel |
|
|
Quadrilateral e Pixel sono topologicamente equivalenti ma il secondo tipo deve soddisfare ad alcuni vincoli geometrici che impongono che i lati siano paralleli agli assi di riferimento e lati adiacenti siano perpendicolari tra di loro.
Analoghe differenze esistono tra i tipi Hexahedron e Voxel.
Va notato che i tipi Pixel e Voxel corrispondono alle definizioni convenzionali di constant valued picture element e volume element solo nel caso in cui gli attributi sono assegnati alle celle.
3.6 Attributi
Un insieme di attributi può essere associato ai vertici oppure alle celle.
L’accesso agli attributi può avvenire mediante gli opportuni indici o attraverso la posizione spaziale. In questo caso per gli attributi associati ai vertici il risultato viene ottenuto interpolando i valori nei vertici adiacenti alla posizione specificata, per gli attributi associati alle celle si restituisce il valore relativo alla cella che contiene la posizione specificata, infatti ogni posizione interna ad una cella restituisce lo stesso valore.
Nella versione 2.2 di VTK non è prevista la possibilità di associare attributi ai lati o alle facce di una cella e il tipo di interpolazione supportato è solo quello lineare.
VTK definisce i seguenti tipi di attributi
Tabella 2
|
Tipi di Attributi |
Generali |
VtkScalars |
Scalari |
|
VtkVector |
Vettori a 3 componenti |
||
|
VtkTensors |
Tensori di rango 3 |
||
|
Specifici |
VtkNormals |
Versori |
|
|
VtkTcoords |
Coordinate di Texture |
||
|
VtkFields |
Vettori di vettori |
||
La classe vtkScalars definisce i metodi Set/GetScalar, la classe vtkVectors definisce i metodi Get/SetVector, e così via, in realtà ognuna di queste classi è una interfaccia specializzata di un oggetto vtkDataArray.
VtkDataArray è una classe virtuale che rappresenta un array dinamico di tuple, le sue sottoclassi concrete si differenziano in base al tipo delle tuple e forniscono metodi di accesso ottimizzati per i diversi casi.
Grazie a questo ogni tipo di attributo dispone del metodo SetDataTypeTo() che permette di specificare il tipo da usare nella rappresentazione.
Si può scegliere tra bit, char, short, int e long float o double, i tipi interi nelle versioni signed e unsigned.
Le disponibilità dei vari tipi base favorisce l’uso della sola memoria necessaria e facilita il mapping di dati esterni sulle rappresentazioni, durante il normale accesso agli attributi però il tipo usato nella rappresentazione viene sempre convertito a float, questo rende più semplice la scrittura dei filtri.
Non è prevista una classe vtkColors, i colori sono rappresentati mediante gli scalari che possono avere più componenti fino ad un massimo di quattro, gestiti mediante i metodi SetNumberOfComponents() e SetActiveComponent().
Sono supportate diverse codifiche dei colori compresa la codifica RGBA.
La seguente linea di codice mostra uno dei modi possibili per accedere ad uno scalare associato ad un certo vertice, la figura che segue mostra tutte le classi coinvolte da questa operazione.
Figura 1‑8
Classi coinvolte da una interrogazione degli attributi
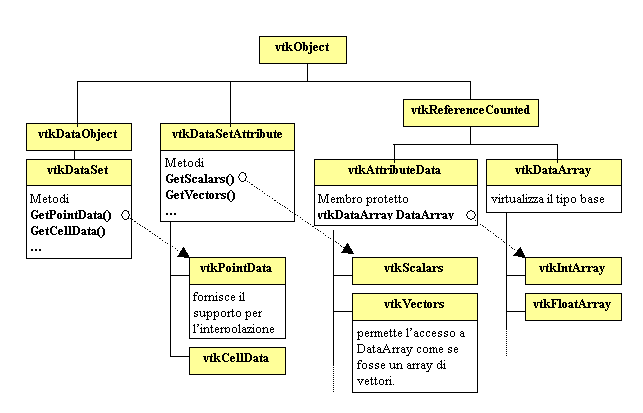
Float s =
un_dataset->GetPointData()->GetScalars()->GetScalar(id_vertice);
3.7 Tipi concreti di DataSet
Di seguito sono riportate le cinque classi derivate da vtkDataSet, ciascuna di queste si distingue per il diverso modo di rappresentare topologia e geometria.
|
|
vtkStructuredPoints
Collezione di punti e celle che formano un reticolo regolare con righe, colonne e facce parallele agli assi di riferimento, può convenientemente rappresentare vettori (1D), immagini (2D) o volumi (3D).
Topologia e Geometria sono regolari e rappresentate in forma implicita.
La geometria viene specificata mediante i metodi SetOrigin, SetSpacing e SetDimensions, la topologia è implicata dalle dimensioni specificate, a seconda dei casi le celle sono di tipo line (1D), pixel (2D) o voxel (3D).
Sulle celle e sui vertici è definito un ordinamento implicito, è possibile accedere alle entità tramite indici o tramite coordinate di reticolo.
Questa struttura è molto comune e viene in genere utilizzata per rappresentare immagini o dati MRI o TAC.
|
|
vtkRectilinearGrid
Analogo al precedente, rilascia il vincolo che i vertici siano equidistanziati.
La geometria è parzialmente regolare, mediante i metodi SetXCoords, SetYCoords e SetZCoords si specificano tre liste di coordinate, ogni combinazione di coordinate x, y, z definisce un vertice.
|
|
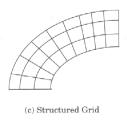
vtkStructuredGrid
È ancora un reticolo analogo a vtkStructuredPoints, ma la geometria viene rappresentata esplicitamente, di conseguenza la griglia può essere liberamente deformata in qualunque configurazione, purché le celle non vengano a sovrapporsi o autointersecarsi.
Metodi specifici di questa classe sono SetPoints mediante il quale si fornisce la lista dei vertici e SetDimensions che stabilisce le dimensioni del reticolo.
Questo tipo di struttura è comune nell’analisi alle differenze finite (PDE)
|
|
VtkPolyData
Geometria e topologia sono entrambe rappresentate in modo esplicito.
I vertici sono rappresentati mediante una lista di punti, le celle sono rappresentate mediante quattro oggetti di tipo vtkCellArray che sono:
Verts – dove sono inserite le celle di tipo vertex e polyvertex
Lines – contiene line e polyline
Polys – contiene triangle, quadrilateral e poligon
Strips – contiene solo i triangle-strip
Gli oggetti vtkCellArray contengono una lista di connectivity list, ciascuna preceduta dalla propria lunghezza, il tipo della cella non viene rappresentato esplicitamente ma viene inferito dalla lunghezza e dalla lista dove è inserita.
I tipi di celle che non sono stati menzionati non sono permessi in questa struttura.
|
|
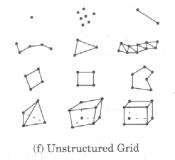
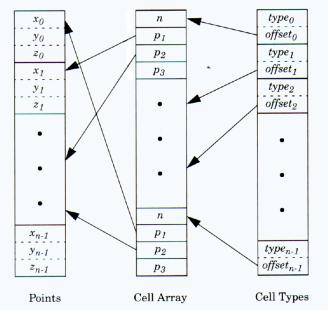
vtkUnstructuredGrid
Questa è la forma di DataSet più generale e la più costosa in termini di organizzazione, quindi va impiegata solo quando è necessario. Geometria e topologia sono entrambe esplicite, ogni tipo di cella definito può venire rappresentato.
La rappresentazione interna delle celle è diversa rispetto a quella usata in vtkPolyData, si usa un unico oggetto vtkCellArray per mantenere tutte le connectivity list ed un oggetto di tipo vtkCellTypes per rappresentare esplicitamente il tipo delle celle. In particolare VtkCellTypes è un array in cui ogni cella è rappresentata da una coppia tipo-cella e posizione della relativa connectivity list.
|
Figura 1‑9: Strutture utilizzate in vtkUnstructuredGrid |
Questi tipi di strutture hanno riscontro nell’ambito dell’analisi agli elementi finiti (FEM)
3.8 Tecniche di visualizzazione
Questo paragrafo illustra come, mediante VTK, si possono applicare le tecniche descritte nel Capitolo 1, e ne introduce di nuove. La descrizione comunque si limita ai filtri usati nell’ambito della tesi che sono solo una parte di quelli presenti nel VTK.
Color
Mapping
Il più semplice modo di visualizzare i valori contenuti negli attributi è quello di metterli in corrispondenza con un insieme di colori ed assegnare questi colori ai punti della superficie dell’oggetto. Il mapping degli attributi è realizzato dalla classe vtkLookupTable che deve essere assegnata all’oggetto Mapper.
Usando la codifica RGBA è possibile intervenire anche sulla trasparenza dell’oggetto.
Contouring
Un’altra comune tecnica di visualizzazione è quella dell’estrazione dei contorni, i contorni estratti da un oggetto bidimensionale sono detti isolinee, ne sono un esempio le curve di livello delle carte geografiche, i contorni estratti da un oggetto tridimensionale sono detti isosuperfici, l’esempio classico è quello dell’estrazione della superficie della pelle a partire da un insieme di dati TAC.
L’estrazione dei contorni è realizzata dalla classe vtkContourFilter che accetta un qualsiasi tipo di DataSet e restituisce un oggetto di tipo PolyData. Esistono diversi tipi di estrattori di contorni come ad esempio il Marching Cubes ed il Marching Squares; vtkContourFilter si occupa di istanziare localmente il tipo di filtro più adatto a seconda del tipo di dato passato in input.
i contorni possono essere tracciati in corrispondenza di uno o più valori degli scalari.
Glyphsing
E’ di visualizzazione che rappresenta i dati mediante simboli, detti glyph; ad esempio mediante vtkHedgeHog è possibile rappresentare vettori mediante delle linee nello spazio. Un Filtro più sofisticato è vtkGlyphs3D, che è il primo filtro che vediamoavere due ingressi.
Mediante il secondo ingresso possiamo specificare come glyph un qualunque oggetto di tipo PolyData, questo oggetto viene replicato in corrispondenza di tutti i vertici del DataSet in Input e può essere colorato, scalato, ed orientato in modo dipendente dai valori contenuti negli scalari, nei vettori o nelle normali.
Cutting
Mediante il cutting si possono estrarre sezioni di un dataset, le sezioni possono poi essere rappresentate con una delle tecniche precedenti.
L’oggetto vtkCutter permette di specificare la sezione da estrarre mediante un oggetto di tipo vtkImplicitFunction Si possono specificare uno o più valori della funzione implicita in corrispondenza dei quali eseguire il taglio.
Probing
Per esplorare un DataSet può essere interessante osservarne gli attributi in corrispondenza di una posizione specificata interattivamente, per questo scopo si può dotare l’interfaccia di un cursore 3D e usare un oggetto vtkProbeFilter.
I due ingressi di questo filtro ricevono qualunque tipo di DataSet e sono indicati come input e source, il primo rappresenta i punti usati come “sonda”, il secondo gli attributi che vengono “sondati”, il DataSet prodotto in uscita conserva geometria e topologia dell’input e contiene gli attributi derivati dal source.
Un altro utilizzo di questo filtro e’ quello che permette di ricampionare un intero Dataset, ad esempio per portarne gli attributi sopra una struttura di diverso tipo.
I Risultati ottenuti mediante il Probing e il Cutting possono essere analoghi, cio’ risulta evidente se si pensa di tagliare e sondare mediante lo stesso piano, la differenza e’ che con il Probing l’oggetto prodotto conserva la topologia della sonda, con il Cutting la topologia dipende da quella dell’oggetto sezionato.
Warping
Un uso frequente degli StructuredPoints e’ quello di rappresentare valori di quote sotto forma di immagini, in questi casi e’ comune deformare l’immagine in modo da produrre una corretta rappresentazione tridimensionale.
Le due classi vtkWarpVectors e vtkWarpScalars alterano la geometria del DataSet in input basandosi sulle informazioni presenti negli scalari e nei vettori rispettivamente, nel primo caso occorre anche specificare la direzione della deformazione.
Questi filtri possono essere applicati soltanto a DataSet con geometria esplicita, quindi a tutti i discendenti di vtkPointSet
Generazione
delle Normali
Quando si visualizza una superficie poligonale mediante un rendering di tipo “flat” i bordi delle singole celle sono chiaramente visibili, per migliorare l’aspetto della superficie si puo’ usare un rendering di tipo Gouraud.
Questo tipo di rendering richiede la presenza delle normali che possono essere calcolate mediante la classe vtkPolyDataNormals. Non sempre si desidera nascondere tutti i bordi, solitamente questi vengono classificati in caratteristici o meno misurando l’angolo formato dalle due facce che vi incidono, il parametro FeatureEdge stabilisce la soglia tra i due casi. Per essere certi che i bordi caratteristici siano sempre visibili nettamente si puo’ attivare l’opzione di Splitting che duplica i vertici interessati da questi bordi e separa le facce sui lati opposti.
Decimazione
Le superfici poligonali e in particolare quelle prodotte dagli algoritmi di tipo Marching Cubes sono sovente composte da un numero molto elevato di poligoni e quindi richiedono lunghi tempi per il rendering limitando la possibilita di farne una visualizzazione interattiva.
Le tecniche di decimazione hanno lo scopo di ridurre il numero di poligoni che compongono una superficie senza alterarne troppo l’aspetto, ovvero di costruirne una nuova piu’ leggera e che sia una buona approssimazione dell’originale.
Le classi che implementano la decimazione sono vtkDecimate e vtkDecimatePro.
Queste classi lavorano solo su superfici composte da triangoli, se questo non e’ il caso a monte si può inserire un oggetto vtkTriangleFilter.
Un altro modo, certamente meno efficace, per ridurre le dimensioni e sveltire il rendering di una superficie e’ quello di convertirne i poligoni in Triangle Strips mediante la classe vtkStripper, questo approccio e’ adatto quando l’obbiettivo da raggiungere non e’ molto lontano.
Mesh
Smooth
Le superfici poligonali possono risultare affette da rumore o presentare una eccessiva rugosità che degrada la qualità delle immagini prodotte e rende più difficile l’eventuale l’applicazione della decimazione.
Questi artefatti possono essere dovuti a fenomeni di aliasing derivanti dall’estrazione di superfici da dati a bassa risoluzione.
Il Filtro vtkSmoothPolyDataFilter tenta di rimediare a questi inconvenienti spostando i vertici in modo da minimizzare il rumore contenuto nella superficie.
Picking
Diversamente dalle precedenti, questa non e’ una tecnica per l’elaborazione dei dati ma di supporto all’interazione. Il Picking permette di selezionare entita’ visualizzate nella scena in base alle coordinate di schermo, queste ultime sono tipicamente specificate con un click del mouse.
La classe vtkPicker serve per selezionare un attore e implementa i metodi Pick e GetActor. Al metodo Pick si passano le coordinate di schermo e il Renderer usato per visualizzare la scena, se ritorna il valore true il picking ha avuto successo e GetActor restituisce l’attore selezionato.
Il Picking e’ realizzato proiettando nella scena una linea dalla telecamera al punto specificato, se questa linea interseca piu’ attori si sceglie quello piu’ vicino alla telecamera.
In modo analogo funzionano le classi vtkPointPicker e vtkCellPicker, che pero’ per la maggiore complessita’ del compito risultano piu’ lente.
Un oggetto vtkPicker e’ istanziato per default dalla classe vtkRenderWindowInteractor e seleziona l’attore sotto il cursore del mouse premendo la lettera ‘p’.
3.9 Formati Supportati
Quattro classi VTK provvedono all’accesso dei file, la coppia Reader/Writer tratta i file che contengono dati, quindi un oggetto solo, la coppia Importer/Exporter file che descrivono una scena cioè attori, camera e luci.
VTK dispone di un proprio formato nativo tramite il quale è possibile salvare e caricare tutti i tipi di DataSet, inoltre sono supportati i formati BYU,STL (stereo lithography), IV (Open Inventor), BMP,TIFF e PNM.
Si possono leggere file 3DS (3D Studio) e CYB (Cyberware) ed esportare una scena in formato VRML.
L’oggetto vtkSLCReader, pensato per leggere Slices, permette di leggere una sequenza di generiche immagini RAW specificando la rapppresentazione dei pixel e la lunghezza dell’header.