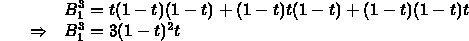Constructing Curve Segments

Linear blend:

• Line segment from an affine combination of points

  

Quadratic blend:

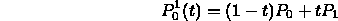
• Quadratic segment from an affine combination of line segments

  

Cubic blend:

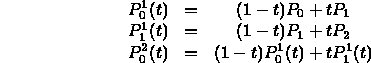
• Cubic segment from an affine combination of quadratic segments

  

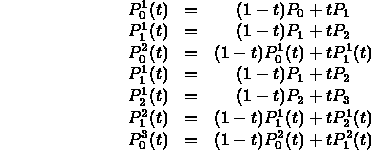
• The pattern should be evident for higher degrees.

Geometric view (deCasteljau Algorithm):

• Join the points 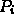by line segments
• Join the t : (1-t) points of those line segments by line segments
• Repeat as necessary
• The t : (1-t) point on the final line segment is a point on the curve
• The final line segment is tangent to the curve at t

Expanding Terms (Basis Polynomials):

• The original points appear as coefficients of Bernstein polynomials

  

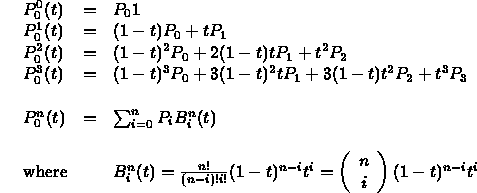
• The Bernstein polynomials of degree n form a basis for the space of all degree-n polynomials

Recursive evaluation schemes:

• To obtain curve points:
  • Start with given points and form succesive, pairwise, affine combinations

    

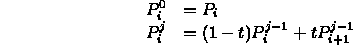
  • The generated points 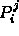are the deCasteljau points
• To obtain basis polynomials:
  • Start with 1 and form successive, pairwise, affine combinations

    

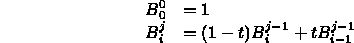
    where 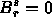when r<0 or r>s

Recursive triangle diagrams (upward):

Computing deCasteljau points

• Each node gets the affine combination of the two nodes entering from below
  • Leaf nodes have the value of their respective points

  

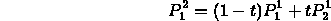
• Each node gets the sum of the path products entering from below

  

Recursive triangle diagrams (downward):

Computing Bernstein (basis) polynomials

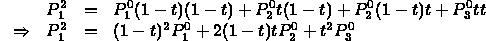
• Each node gets the affine combination of the two nodes entering from above
  • Root node has value 1
  • For other nodes, missing entries above count as zero
• Each node gets the sum of the path products entering from above