- The control polygon is the polygonal mesh with vertices
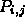
- The patch basis functions are products of curve basis functions
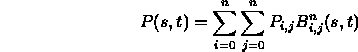
where
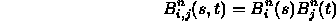
- Patch basis functions sum to one
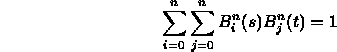
- Patch basis functions are nonnegative on
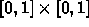
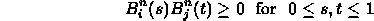
-
- Surface patch is in the convex hull
of the control points
-
- Surface patch is affinely invariant
(Transform the patch by transforming the control points)
-
- As for curves in each variable separately and independently
- Tangent plane is not produced!
- Normals must be computed from partial derivatives.
- Ordinary derivative in each variable separately:
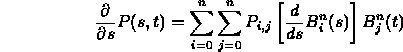
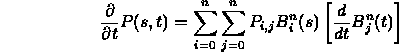
- Each of the above is a tangent vector in a parametric direction
- Surface is regular at each (s,t) where these two vectors are linearly independent
- The (unnormalized) surface normal is given at any regular point by
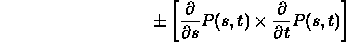
(the sign dictates what is the outward pointing normal)
- In particular, the cross-boundary tangent is given by
(e.g. for the s=0 boundary):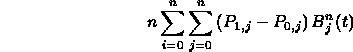
- (and similarly for the other boundaries)
- Can be achieved by ensuring that
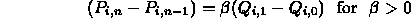
- (and correspondingly for the other boundaries)
- Divide up into polygons:
- A.
- By stepping
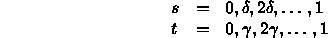
- and joining up sides and diagonals to produce a triangular mesh
- B.
- By subdividing and rendering the control polygon