


Next: Projective Space
Up: Splines
Previous: Spline Continuity
- General B-Splines
-
- Nonuniform B-splines (NUBS) generalize this construction
- A B-spline,
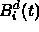 , is a piecewise polynomial:
, is a piecewise polynomial:
- each of its segments is of degree
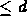
- it is defined for all t
- its segmentation is give by knots
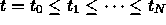
- it is zero for
 and
and 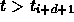
- it may have a discontinuity in its d-k+1 derivative at
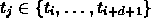 ,
,
if 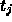 has multiplicity k
has multiplicity k
- it is nonnegative for
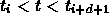
-
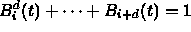 for
for 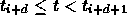 ,
,
and all other 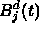 are zero on this interval
are zero on this interval
- Bézier blending functions are the special case where
all knots have multiplicity d+1
- Example (Quadratic):
-
- Evaluation
-
- There is an efficient, recursive evaluation scheme for any curve point
- It generalizes the triangle scheme (de Casteljau) for Bézier curves
- Example (for cubics and
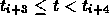 ):
):
CS488/688: Introduction to Interactive Computer Graphics
University of Waterloo
Computer Graphics Lab
cs488@cgl.uwaterloo.ca
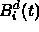 , is a piecewise polynomial:
, is a piecewise polynomial:
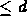
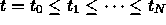
 and
and 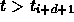
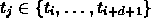 ,
,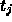 has multiplicity k
has multiplicity k
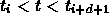
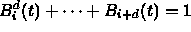 for
for 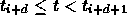 ,
,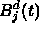 are zero on this interval
are zero on this interval
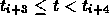 ):
):