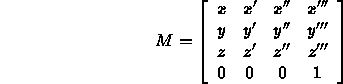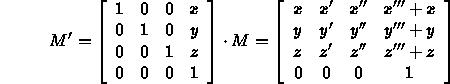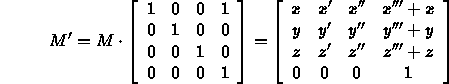- Call the standard frame the world frame.
- The world frame is typically right handed.
- Our scene description is specified in terms of the world frame.
- Often, x to the right, y up, and z straight ahead.
- z is called the viewing direction.
- Note that this is a left handed coordinate system.
- We could instead specify z and y as vectors
- z is the the view direction.
- y is the up vector.
- Compute
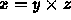
- Get a right handed coordinate system.
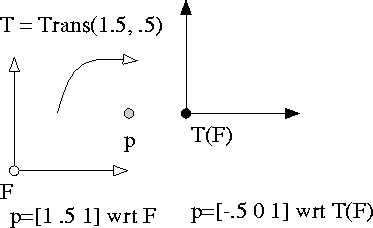
- We can do a change of basis
- Specify a frame relative to the viewer.
- Change coordinates to this frame.
- Usually place a clipping ``box'' around the scene.
- Box oriented relative to the viewing frame.
- Squashes 3D onto 2D, where we can do the window-to-viewport map.
- The projection of the clipping box is used as the window.
![]()
we map ![]() onto
onto
![]()
as follows:
![]()
or if we ignore the frames,
![]()
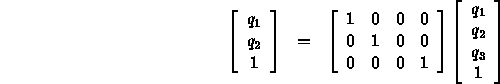
 \
\