


Next: 3D Rotation User
Up: 3D Rotation Specification
Previous: 3D Rotation Specification
- Can derive the matrix for angle-axis rotation by
composing basic transformations.
- Rotation given by
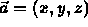 and
and 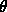 .
.
- Assume that
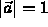 .
.
- General idea: Map
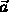 onto one of the canonical axes,
onto one of the canonical axes,
rotate by 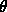 , map back.
, map back.
- Pick the closest axis to
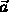 using
using
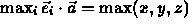 .
.
(Assume we chose the x-axis in the following).
- Project
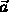 onto
onto 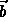 in the xz plane:
in the xz plane:

- Compute
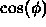 and
and 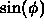 , where
, where
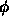 is the angle of
is the angle of 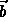 with the x-axis.
with the x-axis.

- Use
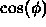 and
and 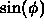 to create
to create 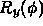 :
:
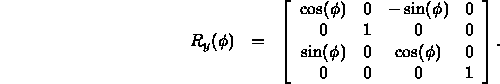
- Rotate
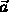 onto the xy plane using
onto the xy plane using 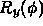 :
:

- Compute
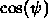 and
and 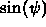 , where
, where
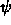 is the angle of
is the angle of 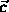 with the x-axis.
with the x-axis.
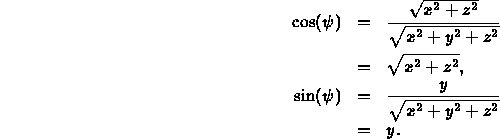
- Use
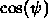 and
and 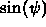 to create
to create 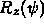 :
:
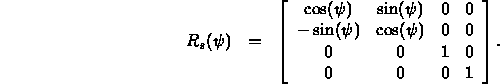
- Rotate
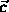 onto the x axis using
onto the x axis using 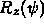 .
.
- Rotate about the x-axis by
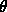 :
: 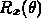 .
.
- Reverse z-axis rotation:
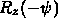 .
.
- Reverse y-axis rotation:
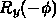 .
.
The overall transformation is
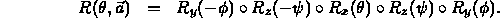
CS488/688: Introduction to Interactive Computer Graphics
University of Waterloo
Computer Graphics Lab
cs488@cgl.uwaterloo.ca
![]()


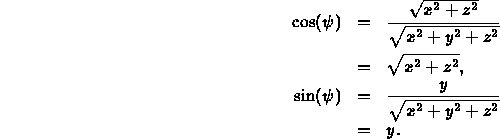
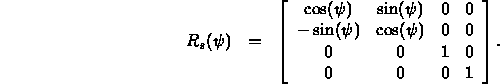
![]()