Intersection Computations

General Issues:

• Ray: express in parametric form

  

  where E is the eyepoint and P is the pixel point

• Scene Object: direct implicit form
  • express as f(Q)=0 when Q is a surface point, where f is a given formula
  • intersection computation is an equation to solve:
    find t such that f(E+t(P-E))=0
• Scene Object: procedural implicit form
  • f is not a given formula
  • f is only defined procedurally
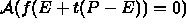  • yields t, where A is a root finding method
    (secant, Newton, bisection, ...)

Quadric Surfaces:

• Surface given by

  

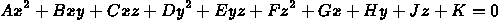
• Ray given by

  

• Substitute ray x,y,z into surface formula
  • quadratic equation results for t
  • organize expression terms for numerical accuracy; ie. to avoid
    • cancellation
    • combinations of numbers with widely different magnitudes

Polygons:

• The plane of the polygon should be known

  

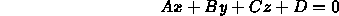
  • (A,B,C,0) is the normal vector
  • pick three succesive vertices

    

  • should subtend a ``reasonable'' angle
    (bounded away from 0 or 180 degrees)
  • normal vector is the cross product
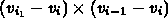
  • D = -(Ax+By+Cz) for any vertex (x,y,z,1) of the polygon
• Substitute ray x,y,z into surface formula
  • linear equation results for t
• Solution provides planar point
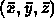
  • is this inside or outside the polygon?

Planar Coordinates:

• Take origin point and two independent vectors on the plane

  

• Express any point in the plane as

  

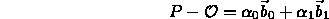
  • intersection point is
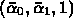
  • clipping algorithm against polygon edges in these 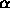coordinates

Alternatives:

Must this all be done in world coordinates?

• Alternative: Intersections in model space
  • form normals and planar coordinates in model space and store with model
  • backtransform the ray into model space using inverse modeling transformations
  • perform the intersection and illumination calculations
• Alternative: Intersections in world space
  • form normals and planar coordinates in model space and store
  • forward transform using modeling transformations